- 條件充分性判斷 已知袋中有紅、黑、白三球若干個(gè)，紅球最多。（） （1）隨機(jī)取出一球是白球的概率為2/5 （2）隨機(jī)取出兩球，兩球中至少一黑的概率小于1/5
- A 、條件（1）充分，但條件（2）不充分
- B 、條件（2）充分，但條件（1）不充分
- C 、條件（1）和（2）單獨(dú)都不充分，但條件（1）和條件（2）聯(lián)合起來(lái)充分
- D 、條件（1）充分，條件（2）也充分
- E 、條件（1）和（2）單獨(dú)都不充分，條件（1）和條件（2）聯(lián)合起來(lái)也不充分
掃碼下載億題庫(kù)
精準(zhǔn)題庫(kù)快速提分
參考答案【正確答案：C】
條件（1）：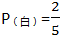
，無(wú)法確定黑球、紅球的數(shù)量比例，故條件（1）不充分。
條件（2）：
，不能確定白球的數(shù)量比例，因此條件（2）也不充分。
聯(lián)合條件（1）和條件（2）：設(shè)黑球有k個(gè)，總數(shù)有5個(gè)，則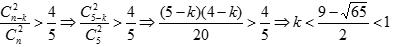
，而白球有2個(gè)，則紅球必大于2個(gè)，即數(shù)量最多。因此，聯(lián)合充分。
您可能感興趣的試題- 1 【問(wèn)題求解】一個(gè)水池，上部裝有若干同樣粗細(xì)的進(jìn)水管，底部裝有一個(gè)常開(kāi)的排水管，當(dāng)打開(kāi)4個(gè)進(jìn)水管時(shí)，需要4小時(shí)才能注滿(mǎn)水池；當(dāng)打開(kāi)3個(gè)進(jìn)水管時(shí)，需要8個(gè)小時(shí)才能注滿(mǎn)水池。現(xiàn)在需要2個(gè)小時(shí)內(nèi)將水池注滿(mǎn)，至少要打開(kāi)進(jìn)水管（）個(gè)。
- A 、8
- B 、7
- C 、6
- D 、5
- E 、4
- 2 【條件充分性判斷】 已知a>0，b>0，ab=8，則當(dāng)a=n時(shí)，
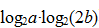取得最大值。（） （1）n=2 （2）n=4 - A 、條件（1）充分，但條件（2）不充分
- B 、條件（2）充分，但條件（1）不充分
- C 、條件（1）和條件（2）單獨(dú)都不充分，但條件（1）和條件（2）聯(lián)合起來(lái)充分
- D 、條件（1）充分，條件（2）也充分
- E 、條件（1）和條件（2）單獨(dú)都不充分，條件（1）和條件（2）聯(lián)合起來(lái)也不充分
- 3 【條件充分性判斷】 在一個(gè)不透明的布袋中裝有2個(gè)白球、m個(gè)黃球和若干個(gè)黑球，它們只有顏色不同，則m=3。（） （1）從布袋中隨機(jī)摸出一個(gè)球，摸到白球的概率是0.2 （2）從布袋中隨機(jī)摸出一個(gè)球，摸到黃球的概率是0.3
- A 、條件（1）充分，但條件（2）不充分
- B 、條件（2）充分，但條件（1）不充分
- C 、條件（1）和（2）單獨(dú)都不充分，但條件（1）和條件（2）聯(lián)合起來(lái)充分
- D 、條件（1）充分，條件（2）也充分
- E 、條件（1）和（2）單獨(dú)都不充分，條件（1）和條件（2）聯(lián)合起來(lái)也不充分
- 4 【問(wèn)題求解】已知
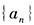為等差數(shù)列，若
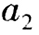與
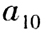是方程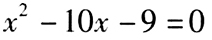
的兩個(gè)根，則
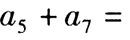（）。 - A 、-10
- B 、-9
- C 、9
- D 、10
- E 、12
- 5 【條件充分性判斷】已知袋中有紅、黑、白三種顏色的球若干個(gè)，則紅球最多。（） （1）隨機(jī)取出的一球是白球的概率為
（2）隨機(jī)取出的兩球中至少有一個(gè)黑球的概率小于
- A 、條件（1）充分，但條件（2）不充分
- B 、條件（2）充分，但條件（1）不充分
- C 、條件（1）和（2）單獨(dú)都不充分，但條件（1）和條件（2）聯(lián)合起來(lái)充分
- D 、條件（1）充分，條件（2）也充分
- E 、條件（1）和（2）單獨(dú)都不充分，條件（1）和條件（2）聯(lián)合起來(lái)也不充分
- 6 【條件充分性判斷】已知
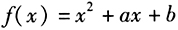，則0≤f（1）≤1。（） （1）f（x）在區(qū)間[0，1]中有兩個(gè)零點(diǎn) （2）f（x）在區(qū)間[1，2]中有兩個(gè)零點(diǎn) - A 、條件（1）充分，但條件（2）不充分
- B 、條件（2）充分，但條件（1）不充分
- C 、條件（1）和（2）單獨(dú)都不充分，但條件（1）和條件（2）聯(lián)合起來(lái)充分
- D 、條件（1）充分，條件（2）也充分
- E 、條件（1）和（2）單獨(dú)都不充分，條件（1）和條件（2）聯(lián)合起來(lái)也不充分
- 7 【問(wèn)題求解】已知方程
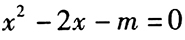有兩個(gè)不相等的正根，則m的取值范圍是（）。 - A 、m>0
- B 、m<1
- C 、-1
- D 、m<-1
- E 、0
- 8 【問(wèn)題求解】已知
，則多項(xiàng)式
的值為（）。 - A 、1
- B 、2
- C 、-1
- D 、0
- E 、±1
- 9 【問(wèn)題求解】已知
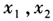是方程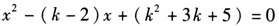
的兩個(gè)實(shí)數(shù)根，則
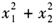的最大值為（）。 - A 、18
- B 、31
- C 、50/9
- D 、50
- 10 【問(wèn)題求解】設(shè)某家庭有3個(gè)孩子，在已知至少有一個(gè)女孩子的條件下，這個(gè)家庭中至少有一個(gè)男孩的概率是（）。
- A 、
- B 、
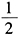
- C 、
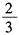
- D 、
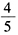
- E 、
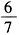
熱門(mén)試題換一換
- 根據(jù)下述材料，寫(xiě)一篇700字左右的論說(shuō)文，題目自擬。 一個(gè)小鎮(zhèn)中，一位商人開(kāi)了一個(gè)加油站，生意特別好。 第二個(gè)來(lái)了，又開(kāi)了一個(gè)加油站，第三個(gè)、第四個(gè)……一陣熱鬧之后，這片很快就又蕭條了。另一個(gè)小鎮(zhèn)，一位商人開(kāi)了一個(gè)加油站，生意特別好。第二個(gè)來(lái)了，開(kāi)了一個(gè)餐廳，第三個(gè)開(kāi)了一個(gè)超市……這片很快就成為了一個(gè)繁華的商業(yè)圈。
- 蟋蟀是一種非常有趣的小動(dòng)物，寧?kù)o的夏夜，草叢中傳來(lái)陣陣清脆悅耳的鳴叫聲，那是蟋蟀在唱歌，蟋蟀優(yōu)美動(dòng)聽(tīng)的歌聲并不是出自它的好嗓子，而是來(lái)自它的翅膀。左右兩翅一張一合，相互摩擦，就可以發(fā)出悅耳的聲響了。蟋蟀還是建筑專(zhuān)家。與它那柔軟的挖掘工具相比，蟋蟀的住宅真可以算得上是偉大的工程了。蟋蟀的住宅門(mén)口，有一個(gè)收拾得非常舒適得平臺(tái)，夏夜，除非下雨或者刮風(fēng)，否則蟋蟀肯定會(huì)在這個(gè)平臺(tái)上唱歌。 根據(jù)以上陳述，以下哪項(xiàng)是蟋蟀在無(wú)雨的夏夜所做的（）。
- Not having a good command of English can be a serious( )preventing you from achieving your goals.
- The boxer（）and almost fell when his opponent hit him.
- 哥本哈根防治地球溫室效應(yīng)會(huì)議，丁院士認(rèn)為，所謂碳排放量與地球氣溫升高的關(guān)系只是某個(gè)西方實(shí)驗(yàn)室通過(guò)計(jì)算機(jī)模擬得出的結(jié)論，算不上科學(xué)主流，而且也沒(méi)有得到證實(shí)。對(duì)此，吳智者認(rèn)為，如果這樣，那么大家根本沒(méi)必要為此花費(fèi)巨大的人力物力財(cái)力聚在一起討論什么減排方案，中國(guó)干脆拒絕參加就好了，沒(méi)必要浪費(fèi)時(shí)間口舌。之所以聚在一起討論，就是至少大家目前是相信這個(gè)模擬數(shù)據(jù)的，盡管將來(lái)有可能會(huì)被推翻或證明是錯(cuò)誤的，但至少目前它是絕大數(shù)科學(xué)家和國(guó)家認(rèn)可的一個(gè)數(shù)據(jù)。 以下哪項(xiàng)如果為真，最能削弱吳智者的論證（）。
- 買(mǎi)4斤蘋(píng)果和5斤梨的價(jià)格之和不小于20元，而買(mǎi)6斤蘋(píng)果和3斤梨的價(jià)格之和不大于24元，則買(mǎi)3斤蘋(píng)果和9斤梨至少需m元。（） （1）m=22 （2）m=27
- 等式成立。（） （1）x＞3 （2）x＜3
- The research of Till Von Wachther suggests that in the recession graduates from elite universities tend to（）.
- 現(xiàn)有一批文字材料需要打印，兩臺(tái)新型打印機(jī)單獨(dú)完成此任務(wù)分別需要4小時(shí)與5小時(shí)，兩臺(tái)舊型打印機(jī)單獨(dú)完成此任務(wù)分別需要9小時(shí)與11小時(shí)，則能在2.5小時(shí)內(nèi)完成此任務(wù)。（） （1）安排兩臺(tái)新型打印機(jī)同時(shí)打印 （2）安排一臺(tái)新型打印機(jī)與兩臺(tái)舊型打印機(jī)同時(shí)打印
- It can be inferred from Paragraph 3 that Christopher Lasch is most probably（）.
億題庫(kù)—讓考試變得更簡(jiǎn)單
已有600萬(wàn)用戶(hù)下載
bgQVa