- 問(wèn)題求解設(shè)A，B，C是三個(gè)相互獨(dú)立的事件，且0＜P （C）＜1，則在下列給出的五對(duì)事件中不相互獨(dú)立的事件是（）。
- A 、
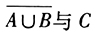
- B 、
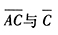
- C 、
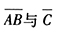
- D 、
- E 、A-AB與C
掃碼下載億題庫(kù)
精準(zhǔn)題庫(kù)快速提分
參考答案【正確答案：B】
若A，B，C是相互獨(dú)立的，則由A，B，C這三個(gè)事件經(jīng)過(guò)事件的運(yùn)算組成的新的事件組中，各事件中不含相同的字母，都是相互獨(dú)立的，在此例中只有選項(xiàng)B。
的，兩事件有相同字母C，從而它們是不獨(dú)立的。
您可能感興趣的試題- 1 【邏輯推理】 相互尊重是相互理解的基礎(chǔ)，相互理解是相互信任的前提；在人與人的相互交往中，自重、自信也是非常重要的，沒(méi)有一個(gè)人尊重不自重的人。沒(méi)有一個(gè)人信任他所不尊重的人。 以上陳述可以推出以下哪項(xiàng)結(jié)論？（）
- A 、不自重的人也不被任何人信任
- B 、相互信任才能相互尊重
- C 、不自信的人也不自重
- D 、不自信的人也不被任何人信任
- E 、不自信的人也不受任何人尊重
- 2 【邏輯推理】相互尊重是相互理解的基礎(chǔ)，相互理解是相互信任的前提；在人與人的相互交往中，自重、自信也是非常重要的，沒(méi)有一個(gè)人尊重不自重的人。沒(méi)有一個(gè)人信任他所不尊重的人。 以上陳述可以推出以下哪項(xiàng)結(jié)論（）。
- A 、不自重的人也不被任何人信任
- B 、相互信任才能相互尊重
- C 、不自信的人也不自重
- D 、不自信的人也不被任何人信任
- E 、不自信的人也不受任何人尊重
- 3 【邏輯推理】相互尊重是相互理解的基礎(chǔ)，相互理解是相互信任的前提；在人與人的相互交往中，自重、自信也是非常重要的，沒(méi)有一個(gè)人尊重不自重的人，沒(méi)有一個(gè)人信任他所不尊重的人。 以上陳述可以推出以下哪項(xiàng)結(jié)論（）。
- A 、不自重的人也不被任何人信任
- B 、相互信任才能相互尊重
- C 、不自信的人也不自重
- D 、不自信的人也不被任何人信任
- E 、不自信的人也不受任何人尊重
- 4 【條件充分性判斷】 一項(xiàng)工作，甲、乙、丙三人各自獨(dú)立完成需要的天數(shù)分別為3，4，6，則丁獨(dú)立完成該項(xiàng)工作需要4天時(shí)間。（） （1）甲、乙、丙、丁四人共同完成該項(xiàng)工作需要1天時(shí)間 （2）甲、乙、丙三人各做1天，剩余部分由丁獨(dú)立完成
- A 、條件（1）充分，但條件（2）不充分
- B 、條件（2）充分，但條件（1）不充分
- C 、條件（1）和（2）單獨(dú)都不充分，但條件（1）和條件（2）聯(lián)合起來(lái)充分
- D 、條件（1）充分，條件（2）也充分
- E 、條件（1）和（2）單獨(dú)都不充分，條件（1）和條件（2）聯(lián)合起來(lái)也不充分
- 5 【簡(jiǎn)答題】三人相鄰（即三個(gè)座位相連）的就座方法共有多少種？
- 6 【條件充分性判斷】A，B，C相互獨(dú)立。（） （1）A，B，C兩兩獨(dú)立 （2）A與BC獨(dú)立
- A 、條件（1）充分，但條件（2）不充分
- B 、條件（2）充分，但條件（1）不充分
- C 、條件（1）和（2）單獨(dú)都不充分，但條件（1）和條件（2）聯(lián)合起來(lái)充分
- D 、條件（1）充分，條件（2）也充分
- E 、條件（1）和（2）單獨(dú)都不充分，條件（1）和條件（2）聯(lián)合起來(lái)也不充分
- 7 【條件充分性判斷】 事件A，B的概率
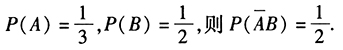。（） （1）
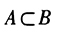（2）A與B互斥 - A 、條件（1）充分，但條件（2）不充分
- B 、條件（2）充分，但條件（1）不充分
- C 、條件（1）和（2）單獨(dú)都不充分，但條件（1）和條件（2）聯(lián)合起來(lái)充分
- D 、條件（1）充分，條件（2）也充分
- E 、條件（1）和（2）單獨(dú)都不充分，條件（1）和條件（2）聯(lián)合起來(lái)也不充分
- 8 【問(wèn)題求解】設(shè)
為三個(gè)獨(dú)立事件，且
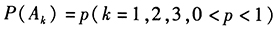，則這三個(gè)事件不全發(fā)生的概率是（）。 - A 、
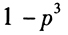
- B 、3（1-p）
- C 、
- D 、
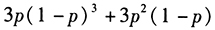
- E 、
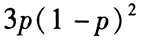
- 9 【條件充分性判斷】事件A與B相互獨(dú)立。（） （1）
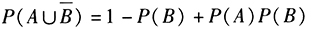（2）事件
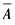與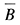
相互獨(dú)立 - A 、條件（1）充分，但條件（2）不充分
- B 、條件（2）充分，但條件（1）不充分
- C 、條件（1）和（2）單獨(dú)都不充分，但條件（1）和條件（2）聯(lián)合起來(lái)充分
- D 、條件（1）充分，條件（2）也充分
- E 、條件（1）和（2）單獨(dú)都不充分，條件（1）和條件（2）聯(lián)合起來(lái)也不充分
- 10 【條件充分性判斷】 隨機(jī)事件A、B相互獨(dú)立。（） （1）P（A∪B）=0 （2）P（AB）=1
- A 、條件（1）充分，但條件（2）不充分
- B 、 條件（2）充分，但條件（1）不充分
- C 、 條件（1）和（2）單獨(dú)都不充分，但條件（1）和條件（2）聯(lián)合起來(lái)充分
- D 、 條件（1）充分，條件（2）也充分
- E 、 條件（1）和（2）單獨(dú)都不充分，條件（1）和條件（2）聯(lián)合起來(lái)也不充分
熱門(mén)試題換一換
- It is too early to say whether IBM's competitors will be able to( )their products to the newhardware at an affordable cost.
- She was made( )at once.
- 對(duì)當(dāng)代學(xué)生來(lái)說(shuō)，德育比智育更重要。學(xué)校的課程設(shè)計(jì)如果不注重培養(yǎng)學(xué)生的完美人格，那么，即使用高薪聘請(qǐng)著名的專家教授，也不能使學(xué)生在面臨道德倫理、價(jià)值觀念挑戰(zhàn)的21世紀(jì)脫穎而出。 以下各項(xiàng)關(guān)于當(dāng)代學(xué)生的斷定都符合上述斷定的原意，除了（）。
- 某省大力發(fā)展旅游產(chǎn)業(yè)，目前已經(jīng)形成東湖、西島、南山三個(gè)旅游景點(diǎn)，每處景點(diǎn)都有二日游、三日游、四日游三種線路。李明、王剛、張波將赴上述三地進(jìn)行9日游。每個(gè)人都設(shè)計(jì)了各自的旅游計(jì)劃。后來(lái)發(fā)現(xiàn)，每處景點(diǎn)他們?nèi)硕歼x擇了不同的線路，李明赴東湖的計(jì)劃天數(shù)與王剛赴西島的計(jì)劃天數(shù)相同。李明赴南山的計(jì)劃是三日游，王剛赴南山的計(jì)劃是四日游。 根據(jù)以上陳述，可以得出以下哪項(xiàng)（）。
- 研究顯示，大多數(shù)有創(chuàng)造性的工程師都有在紙上亂涂亂畫(huà)并記下一些稀奇古怪想法的習(xí)慣。他們的大多數(shù)有價(jià)值的設(shè)計(jì)都直接與這種習(xí)慣有關(guān)。而現(xiàn)在的許多工程師都用計(jì)算機(jī)工作，在紙上亂涂亂畫(huà)不再是一種習(xí)慣。一些專家擔(dān)心，這會(huì)影響工程師的創(chuàng)造性思維，建議在用于工程設(shè)計(jì)的計(jì)算機(jī)程序中匹配模擬的便紙條，能讓使用者在上面涂鴉。 以下哪項(xiàng)最可能是上述建議所假設(shè)的（）。
- 已知a，b，c為三角形的三邊，則ΔABC是等腰三角形。 （） （1）a，b，c為質(zhì)數(shù)，且a+b+c=16 （2）
- 經(jīng)過(guò)兩條直線2x+3y+1 =0和x-3y+4 =0的交點(diǎn)，并且垂直于直線3x +4y -7 =0的直線方程為（）。
- 某公司新進(jìn)李麗、張靜、劉亮、趙強(qiáng)、馬霞、孫明6名員工，分配到三個(gè)部門(mén)，其中兩人分配到市場(chǎng)部，兩人分配到財(cái)務(wù)部，還有兩人分配到公關(guān)部。有關(guān)他們工作分配的情況還需滿足以下條件： （1）李麗分配到市場(chǎng)部，當(dāng)且僅當(dāng)，趙強(qiáng)和張靜都分配到財(cái)務(wù)部； （2）如果孫明不分配到公關(guān)部，那么馬霞分配到財(cái)務(wù)部； （3）如果劉亮分配到財(cái)務(wù)部，則趙強(qiáng)不能分配到財(cái)務(wù)部。 （4）劉亮和馬霞至少有一人不分配到財(cái)務(wù)部。 如果趙強(qiáng)和李麗分配到同一部門(mén)，且張靜分配到財(cái)務(wù)部，那么可以得出以下哪項(xiàng)（）。
- 某餐廳供應(yīng)晚飯，每位顧客可以在餐廳提供的菜肴中任選2葷2素共4種不同的品種，現(xiàn)餐廳準(zhǔn)備了五種不同的葷菜，若要保證每位顧客有200種以上不同的選擇，則餐廳至少還需準(zhǔn)備（）種不同的素菜品種。
- |m-n|=5。（） （1）m和n都是正整數(shù)，m和n的最大公因數(shù)為15，且3m+2n=180 （2）質(zhì)數(shù)m，n滿足5m+7n=129
億題庫(kù)—讓考試變得更簡(jiǎn)單
已有600萬(wàn)用戶下載
LQkOd