2020年MBA考試《數(shù)學》考試共25題，分為問題求解和條件充分性判斷。小編為您整理第九章 排列與組合5道練習題，附答案解析，供您備考練習。

1、將9個人以2，3，4分為三組。【簡答題】

1、某校從8名教師中選派4名教師同時去4個邊遠地區(qū)支教（每地一人），其中甲和乙不同去，甲和丙只能同去或同不去，則不同的選派方案有（）。【問題求解】

A.300種

B.400種

C.500種

D.600種

E.700種

正確答案:D

答案解析:將甲、丙兩人看成是一個元素，有兩種情況，他們去或不去，而甲、乙兩人中又只能選一個人去：
甲被選去時，有；
當甲未被選去時，有；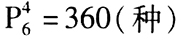
所以共有不同的選法 240+360=600（種）。

1、至多有1只黑球的不同取法共有多少種？【簡答題】

1、可組成多少個允許有重復數(shù)字的三位奇數(shù)？【簡答題】

1、三人相鄰（即三個座位相連）的就座方法共有多少種？【簡答題】

1、n=3。（）
（1）若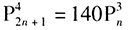
（2）若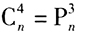【條件充分性判斷】

A.條件（1）充分，但條件（2）不充分

B.條件（2）充分，但條件（1）不充分

C.條件（1）和（2）單獨都不充分，但條件（1）和條件（2）聯(lián)合起來充分

D.條件（1）充分，條件（2）也充分

E.條件（1）和（2）單獨都不充分，條件（1）和條件（2）聯(lián)合起來也不充分

正確答案:A

答案解析:由條件（1），得（2n+1）（2n）（2n-1）（2n-2）=140n（n-1）（n-2），即，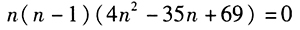
即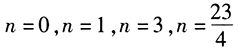，因為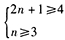且n為整數(shù)，所以n=3，即條件（1）是充分的。
由條件（2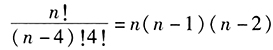），可得 n（n-1）（n-2）（n-3）=24n（n-1）（n-2），整理得：n（n-1）（n-2）（n-3-24）=0，即 n=0，n=1，n=2，n=27。由于n≥4，從而n=27，條件（2）不充分。

1、將9個人以3，3，3分為三組.【簡答題】

1、甲、乙、丙三項任務各需3人，則不同的選派方法共有多少種？【簡答題】

1、某人欲從5種A股票和4種B股票中選購3種，其中至少有2種A股票的買法有（）。【問題求解】

A.40種

B.50種

C.60種

D.65種

E.70種

正確答案:B

答案解析:用加法原理至少有2種A股票的買法可分解為3A或2A1 B。3A的買法有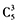種，2A1B的買法有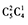種，
從而總的買法有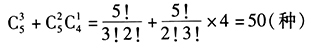

1、N=125。（）
（1）有5本不同的書，從中選出3本送給3名同學，每人一本，共有Ⅳ種不同的選法
（2）書店有5種不同的書，買3本送給3名同學，每人一本，共有Ⅳ種不同的送法【條件充分性判斷】

A.條件（1）充分，但條件（2）不充分

B.條件（2）充分，但條件（1）不充分

C.條件（1）和（2）單獨都不充分，但條件（1）和條件（2）聯(lián)合起來充分

D.條件（1）充分，條件（2）也充分

E.條件（1）和（2）單獨都不充分，條件（1）和條件（2）聯(lián)合起來也不充分

正確答案:B

答案解析:由條件（1）。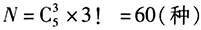
由條件（2），每人必須送一本書且只能送一本書，但同一種書可以送給多個人，此類問題可歸納為分房問題，這里人是“人”，書是“房”，因此不同送法為。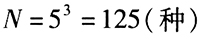

1、“只有1個次品”的抽法有多少種？【簡答題】

1、N=3600。（）
（1）7個人排成一排，甲在排頭的排法共有N種
（2）7個人排成一排，甲不在排頭也不在排尾的排法共有N種【條件充分性判斷】

A.條件（1）充分，但條件（2）不充分

B.條件（2）充分，但條件（1）不充分

C.條件（1）和（2）單獨都不充分，但條件（1）和條件（2）聯(lián)合起來充分

D.條件（1）充分，條件（2）也充分

E.條件（1）和（2）單獨都不充分，條件（1）和條件（2）聯(lián)合起來也不充分

正確答案:B

答案解析:由條件（1），甲在排頭的排法共有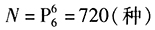，從而條件（1）不充分。
由條件（2），先排甲有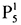種不同方法，再排余下的6人有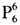種，所以應用乘法原理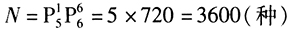，，即條件（2）充分。